Добрый день! Когда мы говорим об орбитах и спутниках, мы обычно представляем их движение по траекториям вокруг планеты, но не сквозь неё. Это логично, ведь обычный аппарат не может физически пролететь сквозь Землю. Однако давайте представим гипотетическую ситуацию: человечество создало спутник из уникального материала, который без какого-либо сопротивления проходит сквозь любые физические тела. Если запустить такой спутник на орбиту, как будет выглядеть его траектория? Именно этот увлекательный вопрос мы и рассмотрим в данной статье.
Физические основы: почему гравитация внутри и снаружи планеты работает по-разному
Чтобы понять, почему траектории движения под землёй и над её поверхностью будут принципиально отличаться, проведём аналогию с электродинамикой. Из школьного курса физики известно: если электрический заряд равномерно распределён по поверхности сферы, то электрическое поле существует только снаружи этой сферы, внутри него нет. Это наглядно иллюстрирует следующая схема:
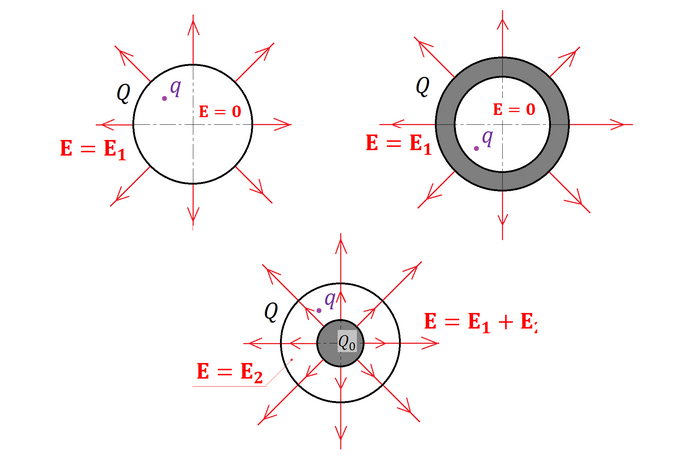
На изображении видно, что силовые линии поля существуют исключительно за пределами сферы. Третья картинка демонстрирует важный момент: если внутри большой заряженной сферы поместить меньшую, то поле внутри большой сферы создаёт только меньший шар.
Теперь представим пробный заряд, движущийся внутри равномерно заряженного по объёму шара. Плотность заряда зависит только от расстояния до центра. Как определить силу, действующую на заряд? Решение заключается в мысленном разделении шара: мы выделяем сферу меньшего радиуса, внутри которой находится наш заряд, и толстостенную сферу большего радиуса, её окружающую.

Зазор между сферами на рисунке показан для наглядности, в реальности он бесконечно мал. Ключевой вывод: на пробный заряд действует гравитационное притяжение только той части массы планеты, которая находится ближе к её центру, чем сам спутник. Внешние слои (толстостенная сфера) в сумме не оказывают на него никакого влияния. Это фундаментальное отличие от движения над поверхностью, где спутник притягивается всей массой планеты.
Почему мы говорим об электричестве, когда речь идёт об орбитах? Всё дело в поразительном сходстве законов. Взгляните на формулы для сил гравитационного и электростатического взаимодействия:
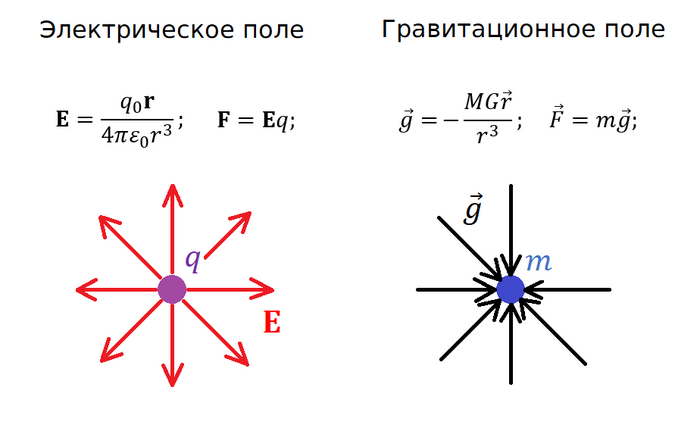
Формулы практически идентичны (отличие в константах и знаке). Это означает, что всё сказанное о зарядах внутри сферы справедливо и для гравитации. Следовательно, на спутник, летящий под землёй, действует гравитация только той части планеты, которая находится «под ним» (ближе к центру). Это знание позволяет нам вывести уравнения движения для подземной орбиты.
Математическое описание: вывод уравнений движения
Для удобства рассмотрим движение в полярной системе координат. Пренебрежём силами сопротивления, так как наш гипотетический спутник проходит сквозь всё без трения. В радиальном направлении (вдоль линии, соединяющей спутник с центром Земли) действуют две силы: гравитационная сила притяжения и центробежная сила.
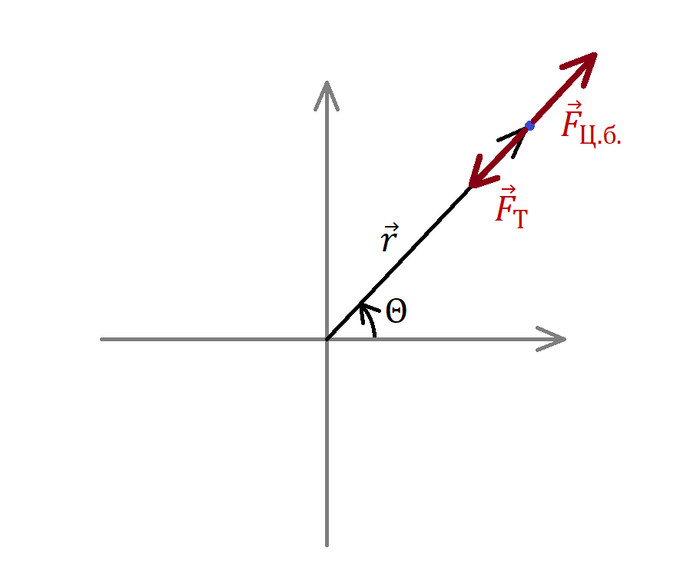
Уравнение движения для радиальной составляющей записывается на основе второго закона Ньютона. Для описания углового движения удобнее всего использовать закон сохранения момента импульса (аналог импульса для вращательного движения). Продифференцировав его и объединив с радиальным уравнением, получаем систему дифференциальных уравнений.
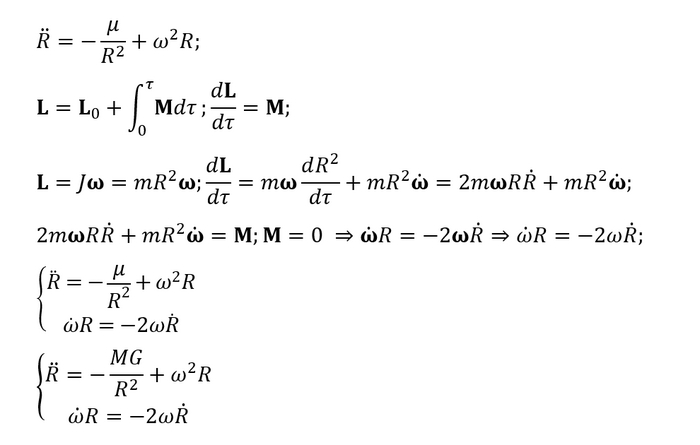
Главная особенность этой системы — функция M(r), которая описывает массу планеты, действующую на спутник на расстоянии r от центра. Эта масса не постоянна и зависит от того, находится ли спутник под или над поверхностью, а также от распределения плотности внутри Земли.
Моделирование орбит для Земли с постоянной плотностью
Начнём с простейшей модели, предположив, что плотность Земли постоянна. В этом случае масса M(r) вычисляется просто как произведение плотности на объём сферы радиусом r.
Кстати о космосе: Американская компания SpaceX в конце 2022 года успешно вывела на орбиту новую партию спутников Starlink с помощью ракеты Falcon 9.
После подстановки этой функции в уравнения и попыток аналитического решения становится ясно, что система не имеет простого решения в элементарных функциях. Однако её можно исследовать численно. Чтобы учесть возможность полёта как под, так и над поверхностью, зададим функцию M(r) кусочно: внутри Земли масса растёт как куб радиуса, а снаружи становится постоянной и равной полной массе планеты.
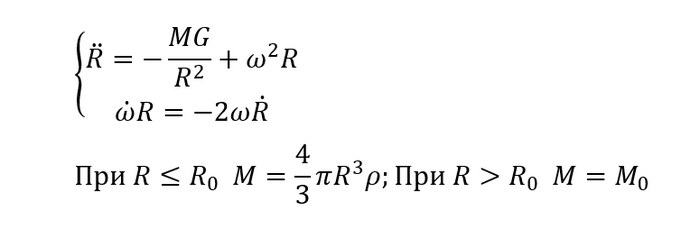
Проведя численное моделирование в Wolfram Mathematica для различных начальных условий, получаем удивительные траектории.
Вот некоторые из полученных графиков:
Результаты моделирования показывают интересные закономерности:
- Если спутник движется полностью под поверхностью Земли, его орбита представляет собой эллипс, центр которого совпадает с центром планеты.
- Если траектория проходит и под, и над поверхностью, она становится сложной. Её можно представить как чередование участков: под землёй — эллипс с центром в центре Земли, над землёй — обычный кеплеровский эллипс с фокусом в центре Земли. Визуально это выглядит как вращающаяся (прецессирующая) орбита. Если большая часть пути проходит под землёй, вращается «подземный» эллипс; если над — вращается «надземный».
Более реалистичная модель: орбиты с учётом реального распределения плотности Земли
В действительности плотность земных недр меняется с глубиной: от коры к ядру она возрастает. Это необходимо учесть для более точной картины. Уравнения движения остаются прежними, но функция M(r) становится значительно сложнее.
Для построения функции плотности был использован график из научного источника, отображающий зависимость плотности от глубины.
Источник изображения
С помощью интерполяции данных с графика была создана кусочно-заданная функция плотности, а затем, путём интегрирования, — функция массы M(r). Чтобы ускорить расчёты в Wolfram, функция массы была предварительно вычислена в нескольких десятках точек и также аппроксимирована.
Код для вычисления точек функции массы.
После проведения моделирования с переменной плотностью получаются ещё более красивые и сложные траектории.
Результат моделирования — изящные симметричные узоры, которые спутник «рисует» за множество витков.
Общая тенденция сохраняется: траектории остаются близкими к эллипсам, но теперь они прецессируют практически всегда. Центр эллипса по-прежнему близок к центру Земли для «подземных» орбит и смещён к фокусу для «надземных». При достаточно высокой начальной скорости спутник может выйти на гиперболическую траекторию и покинуть окрестности Земли.
Практическая часть: как самостоятельно смоделировать подземные орбиты
Если эти красивые графики вдохновили вас на эксперименты, вы можете повторить расчёты самостоятельно. Ниже приведён готовый код для Wolfram Mathematica, позволяющий строить такие траектории. Просто скопируйте его, задайте свои начальные параметры и запустите.
Для модели с постоянной плотностью:
Сначала выполните инициализацию (один раз):
Mass[R_] := Piecewise[{{4/3*Pi*R^3*5515, R < 6371000}, {5.972*10^24, R >= 6371000}}]; G = 6.6743*10^-11;
Затем для построения графика задайте начальные условия и запустите расчёт:
v0 = 5000; R0 = 3000000; t0 = 100000; {Rsol, Anglesol} = NDSolveValue[{R''[t] == -Mass[R[t]]*G/R[t]^2 + Angle'[t]^2*R[t], Angle''[t]*R[t] == -2*Angle'[t]*R'[t], R[0] == R0, R'[0] == 0, Angle[0] == 0, Angle'[0] == v0/R0}, {R, Angle}, {t, 0, t0}]; ParametricPlot[{Rsol[t]*Cos[Anglesol[t]], Rsol[t]*Sin[Anglesol[t]]}, {t, 0, t0}]Для модели с реальной плотностью Земли:
Код инициализации длиннее, так как содержит интерполяционную таблицу функции массы. Его можно найти в оригинальной статье. После его выполнения используйте тот же блок расчёта траектории, что и выше, подставив свою функциюMass1[R].
В коде вы можете менять три ключевые переменные: v0 (начальная скорость, м/с), R0 (начальное расстояние от центра Земли, м) и t0 (время моделирования, с). Учтите, что код для разных моделей нужно запускать в отдельных документах или сессиях.
Заключение и итоги
На этом наше теоретическое путешествие завершается. Мы рассмотрели гипотетическую, но физически обоснованную задачу о движении спутника, способного проходить сквозь Землю. Были выведены уравнения движения, проанализированы модели для постоянной и переменной плотности планеты и получены визуально впечатляющие траектории. Главный вывод: такие «подземно-надземные» орбиты представляют собой сложные прецессирующие эллипсы, поведение которых кардинально отличается от классических кеплеровских орбит. Надеемся, материал был познавательным, а графика — приятной для глаза. Если остались вопросы — добро пожаловать в комментарии!
Всем удачи и побольше красивых аналитических решений!
Больше интересных статей на тему: Космос.
Источник статьи: Как выглядит орбита спутника под землей?.

